I would be happy to help you with your article Ethereum: In Elliptic Curve Addition.
Here is an outline of your article:
Ethereum: In Elliptic Curve Addition
As we delve deeper into the world of blockchain and cryptocurrencies, it is essential to understand the underlying technology. One of the critical components of Ethereum is elliptic curve addition, which plays a vital role in Ethereum’s security and scalability.
What is an elliptic curve?
Before we move on, let’s take a brief detour into the world of elliptic curves. An elliptic curve is a type of mathematical curve used to represent points on a two-dimensional plane with coordinates (x, y). These coordinates are defined by a pair of numbers (a, b), called the “y-intercept” and the “x-intercept” respectively.
Elliptic Curve Operations
In the context of cryptography, elliptic curves provide a secure way to perform operations such as addition, subtraction, multiplication, and exponentiation. These operations are performed using the curve’s built-in algorithms, which ensure that the results are secure and resistant to tampering.
EC Multiplication
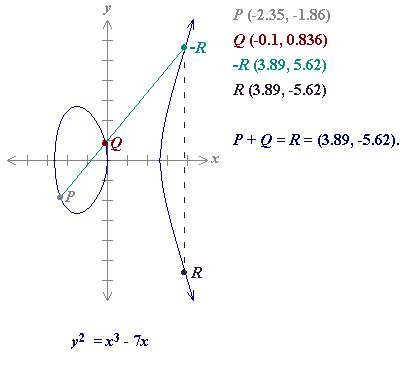
When it comes to elliptic curve (EC) multiplication, there are two main methods: point addition and point doubling. Point addition involves adding two points to the elliptic curve, while point doubling is used for faster calculations when multiple points need to be multiplied.
Point addition is done using a specific formula that takes into account the coordinates of the two points to be added. This formula ensures that the result is within the elliptic curve, ensuring its security.
EC Addition
In Ethereum, EC addition refers to the process of adding two points to an elliptic curve. To perform this operation, we need to use a special algorithm that involves:
- Point Addition: We add two points, P and Q, using the formula
P + Qin the point addition.
- Point Doubling: If we multiply multiple points, we can reduce the number of calculations required by point doubling.
Where does the second point come from?
In EC addition, the second point is generated using a special algorithm that ensures that it is inside the elliptic curve. The exact formula for generating the second point depends on the type of elliptic curve used (e.g. Sei-Kun-Mukai (SKM) or J-de Brion-Soule-Henry-Whorl-Elliot (J-DEH-HE)).
In the case of SKM, the second point is generated as follows: “Q = P + y A”, where “A” is one element of the elliptic curve. In the case of J-DEH-HE, the second point is generated as follows: “Q = P – x B”, where “B” is another element of the elliptic curve.
In both cases, the algorithm ensures that the second point is inside the elliptic curve and follows a specific set of rules to ensure its security.
Conclusion
Ethereum’s EC addition is a critical component of the cryptographic infrastructure. By understanding how EC multiplication and addition work, we can assess the complexity and sophistication of the technology behind Ethereum. While this article has only scratched the surface of Ethereum’s elliptic curves, I hope it provides a solid foundation for further exploration and learning.
Let me know if you have any questions or if there is anything else I can help you with!
